Python provides a few higher order (or functional programming) functions in the standard library that can be quite useful:

map
filter
reduce
lambda
list comprehensions

Picture from SwiftUnboxed

This article series focuses on exploring these. In the previous article we've taken a look at the map function. In this notebook, we'll learn more about the reduce function in Python. Again, I will assume you already know about list expressions, (or more broadly, generator expressions). Just like I got side-tracked exploring exponential function syntax in the previous installment, this time we'll spend some time learning about function composition, and benchmarking various ways of working with function call chains in Python.

This time, reduce() needs to be imported from the standard library with:

In [1]:

from functools import reduce

At this point, an alarm bell might (should?) be going on in your head: If it isn't in base Python, should I really use it on a regular basis? The answer to that is a bit complicated.

Python core developers are opinionated when it comes to it. From the Python 3.0 release notes:

Removed reduce(). Use functools.reduce() if you really need it; however, 99 percent of the time an explicit for loop is more readable.

Here, we'll spend some time exploring the 1% of times it can be useful. If you don't know it exists, you can't use it, right?

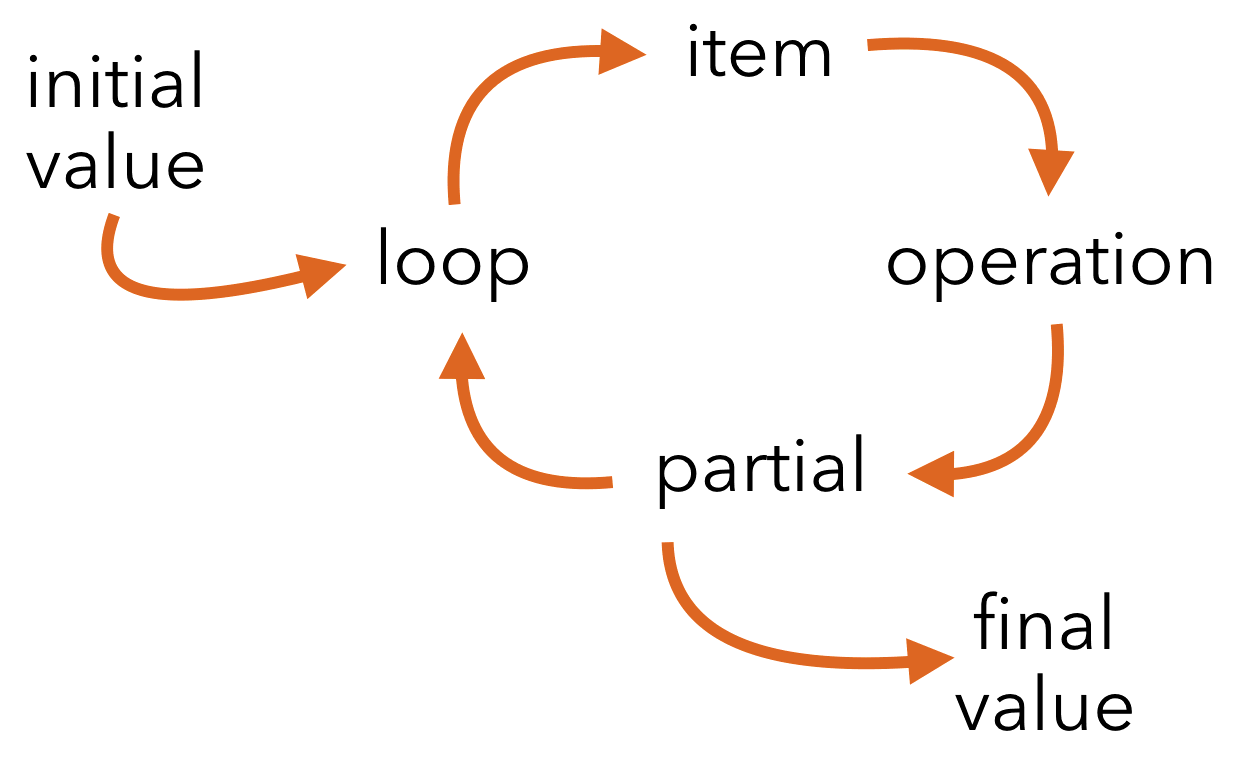
What does reduce even do?¶

Rolling calculations.

Reduce passes the previous output every turn in the loop with the current element. This means that you get some preserved state between iterations and that you can build the output as you need it.

You might have heard of the 'map-reduce' paradigm for distributed data processing, popularized by Big Data applications like Apache Hadoop. Say you have three computers containing sales transactions, and you want to know the sum of sales. We'll get back to this and use it as our motivating example.

In [2]:

help(reduce)

Help on built-in function reduce in module _functools:

reduce(...)
    reduce(function, sequence[, initial]) -> value
    
    Apply a function of two arguments cumulatively to the items of a sequence,
    from left to right, so as to reduce the sequence to a single value.
    For example, reduce(lambda x, y: x+y, [1, 2, 3, 4, 5]) calculates
    ((((1+2)+3)+4)+5).  If initial is present, it is placed before the items
    of the sequence in the calculation, and serves as a default when the
    sequence is empty.

So reduce takes a two-argument function and applies it iteratively. Let's start with a few imports and work our way up to a simple use case.

In [3]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import operator  # base Python functions
from time import time

In [4]:

sales = [75723, 89359, 27503, 42715, 23425, 31931, 64668, 88465, 62016, 90350]

In [5]:

def sum_of_sales(total:int, sale: int):
    return total + sale

In [6]:

reduce(sum_of_sales, sales)

Out[6]:

For simple operations, many people will simply write this as a lambda function:

In [7]:

reduce((lambda x, y: x + y), sales)

Out[7]:

But there's more to it that that. Let's dig into what's actually going on, and see how we might make use of it.

In [8]:

def sum_of_sales(total:int, sale: int):
    print(sale, total)
    return sale + total
    

reduce(sum_of_sales, sales)

89359 75723
27503 165082
42715 192585
23425 235300
31931 258725
64668 290656
88465 355324
62016 443789
90350 505805

Out[8]:

So actually, it's quite like a fancy for-loop in disguise!

The first argument is the 'accumulator' variable, and the second is the one itered on. Of course, these variable exist only in the scope of the function:

In [9]:

try:
    print(total)
except NameError as e:
    print(NameError, e)

<class 'NameError'> name 'total' is not defined

At first, this seems trivial and roundabout way of doing things. Python has a built-in that does JUST that!

In [10]:

sum(sales)

Out[10]:

But for products of items in a list, it does provide a better one-liner than its list comprehension counterpart. Let's say we want to calculate the volume of a 6-dimensional box (an everyday occurrence, for sure! 😉)

In [11]:

box_sides = [4, 2, 6, 7, 8, 2]

volume = 1
for dim in box_sides:
    volume *= dim
print(volume)

Compare that to:

In [12]:

reduce(operator.mul, box_sides)

Out[12]:

or even

In [13]:

reduce(lambda x, y: x * y, box_sides)

Out[13]:

Uses¶

Now, Guido van Rossum, the creator and Benevolent Dictator for Life of Python, has stated previously that:

There aren't a whole lot of associative operators. (Those are operators X for which (a X b) X c equals a X (b X c).) I think it's just about limited to +, *, &, |, ^, and shortcut and/or. We already have sum(); I'd happily trade reduce() for product(), so that takes care of the two most common uses.

So are there any use cases for non-associative use cases? At the risk of turning this part of the article as a rehash of the StackOverflow question Useful code which uses reduce()?, here are the main uses for reduce():

Flattening a list of lists
Getting the intersection of $n$ lists
Turning a list of digits into a number
Least common multiple for 3 or more numbers
Accessing deeply nested items

Each of these use cases in Python has a 'canonical recipe' that does not use reduce(). In fact, let's take a look at them.

Flattening a list of lists¶

In [14]:

lists = [[2, 4, 8], [1, 4, 1231231, 6], [1], [234, 43, 76], [2, 4, 8], [1, 4, 1231231, 6], [1]]

In [15]:

# 'Canonical' answer; can also handle arbitrary levels of nestedness
from collections import Iterable

def flatten(items):
    """Yield items from any nested iterable; see REF."""
    for x in items:
        if isinstance(x, Iterable) and not isinstance(x, (str, bytes)):
            yield from flatten(x)
        else:
            yield x
            
            
list(flatten(lists))

Out[15]:

[2, 4, 8, 1, 4, 1231231, 6, 1, 234, 43, 76, 2, 4, 8, 1, 4, 1231231, 6, 1]

Now with reduce:

In [16]:

reduce(operator.concat, lists)

Out[16]:

[2, 4, 8, 1, 4, 1231231, 6, 1, 234, 43, 76, 2, 4, 8, 1, 4, 1231231, 6, 1]

Getting the intersection of $n$ lists¶

In [17]:

list_items = [['apple', 'pear', 'orange', 'kiwi', 'bicycle'],
               ['shark', 'speedo', 'coconut', 'kiwi', 'bicycle'],
               ['coffee', 'tea', 'apple', 'kiwi', 'bicycle']]

In [18]:

# 'Canonical' answer
set(list_items[0]).intersection(*list_items)

Out[18]:

{'bicycle', 'kiwi'}

In [19]:

# With reduce. Personally, I actually prefer the first expression.
reduce(set.intersection, [set(item) for item in list_items])

Out[19]:

{'bicycle', 'kiwi'}

Turning a list of digits into a number¶

In [20]:

digits = [1, 5, 2, 7, 5, 2, 6, 24]

In [21]:

# 'Canonical' answer
int(''.join(str(i) for i in digits))

Out[21]:

152752624

Compared to

In [22]:

reduce(lambda a,d: 10*a+d, digits, 0)

Out[22]:

15275284

Least common multiple for 2 or more numbers¶

In [23]:

import math


numbers = (100, 25, 6)
reduce(lambda a,b: a * b // math.gcd(a, b), numbers)

Out[23]:

Accessing deeply nested items¶

In this case, reduce actually is the canonical answer to this problem in Python.

In [24]:

data = {
    "a":{
        "r": 1,
        "s": 2,
        "t": 3
        },
    "b":{
        "u": 1,
        "v": {
            "x": 1,
            "y": 2,
            "z": 3
        },
        "w": 3
        }
}

In [25]:

data['b']['v']['y']

Out[25]:

Sometimes you just don't know in advance what the query in the nested dictionnary will be, though. Imagine being given a list of (ordered) keys as your input. This can often happen in web apps and the like. You would write it out like this:

In [26]:

import operator

# The user supplies this
keys = ['b', 'v', 'y']

reduce(operator.getitem, keys, data)

Out[26]:

The killer use-case: function composition¶

As we've seen, reduce is not all that useful except for niche cases, and even then they can be just as readable when written with for loops.

I'd like to leave you with a final use case that I like to keep around.

When running a data processing pipeline, what often happens is a series of function calls that can quickly become unruly. For example:

In [27]:

def clean_strings(string):
    s = string.lower()
    s = s.replace('brown', 'blue')
    s = s.replace('quick', 'slow')
    s = s.replace('lazy', 'industrious')
    s = s.title()
    return s


string = "THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG"
clean_strings(string)

Out[27]:

'The Slow Blue Fox Jumps Over The Industrious Dog'

For one-time use, this could be written as a chained operation instead, by wrapping the expression in parentheses

In [28]:

(string.lower()
       .replace('brown', 'blue')
       .replace('quick', 'slow')
       .replace('lazy', 'industrious')
       .title()
)

Out[28]:

'The Slow Blue Fox Jumps Over The Industrious Dog'

In terms of composability though, it doesn't quite compare to using reduce:

In [29]:

color = lambda x: x.replace('brown', 'blue')
speed = lambda x: x.replace('quick', 'slow')
work = lambda x: x.replace('lazy', 'industrious')

# In actual use cases, this list can get quite lengthy!
transforms = [str.lower, color, speed, work, str.title]

In [30]:

def call(string, function):
    return function(string)

       
reduce(call, transforms, string)

Out[30]:

'The Slow Blue Fox Jumps Over The Industrious Dog'

By splitting the concern of the clean_strings() function, that acts as both:

A container for string cleaning methods, and
The action of actually applying the functions to the string,

we gain added readability and maintainability by having defined what we'll be doing to the string somewhere else than when we apply it, which is neatly done in a single line.

Benchmarks¶

Now the kicker! Is it faster than regular chained calls, though?

Short string, 5 string functions¶

In [31]:

string = "THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG"

In [32]:

%%timeit
(string.lower()
       .replace('brown', 'blue')
       .replace('quick', 'slow')
       .replace('lazy', 'industrious')
       .title()
)

1.7 µs ± 93.4 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

In [33]:

%%timeit
clean_strings(string)

1.88 µs ± 53.5 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

In [34]:

%%timeit
reduce(call, transforms, string)

2.56 µs ± 38.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

So, the answer here is no. 😂

Short string, 50 string functions¶

I'll skip calling the long chained call at this point, and just assume performance will be similar to calling clean_strings(). To do this, we'll define a little helper function so that we can repeat our clean_strings() 10 times.

In [35]:

string = "THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG"

In [36]:

def repeat(func, n, x):
    for i in range(n):
        x = func(x)
    return x

In [37]:

%%timeit
repeat(clean_strings, 10, string)

15.4 µs ± 246 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

In [38]:

%%timeit
reduce(call, transforms * 10, string)

21.6 µs ± 410 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Well, no gains there either!

Long string, 5 string functions¶

And now with a very long string:

In [39]:

string = "THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG" * 1000

In [40]:

%%timeit
(string.lower()
       .replace('brown', 'blue')
       .replace('quick', 'slow')
       .replace('lazy', 'industrious')
       .title()
)

756 µs ± 6.66 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

In [41]:

%%timeit
clean_strings(string)

748 µs ± 6.57 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

In [42]:

%%timeit
reduce(call, transforms, string)

755 µs ± 3.05 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Long string, 50 string functions¶

In [43]:

%%timeit
repeat(clean_strings, 10, string)

6.63 ms ± 67.4 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

In [44]:

%%timeit
reduce(call, transforms * 10, string)

6.64 ms ± 25.1 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

At this point, it looks as though the performance difference between the two methods are due to overhead, rather than execution performance.

Conclusions for function composition¶

So as we can see, there's a cliff when chaining functions where using reduce starts making sense to replace chained function calls, when either:

The number of functions to apply in the chain are high enough to become unreadable, or
You won't know in advance which functions to apply, and need a way to abstract it away.

Genetic Algorithms
Courtesy of [CoalHMM Documentation](https://github.com/birc-aeh/coalhmm)

One example of this last case that comes to mind is if you were running a genetic algorithm experiment to evolve a solution to a problem that uses function composition.

For more on this, I highly recommend you take a look at Mathieu Larose's article entitled Function Composition in Python